分离变量法求解波动方程
一,问题描述
首先,我们需要考虑最简单的一种情形。为了简单期间,以x轴为基准轴,把弦的一段放在原点。
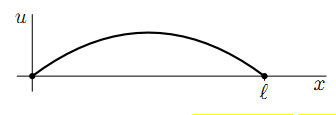
以u(x,t)表示弦l上任意位置在t时刻的小位移量。假如弦只发生很小的横向震动,那么必满足以下方程:
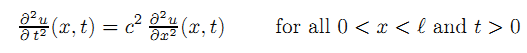
同时,需满足以下条件:
(1)初始条件:
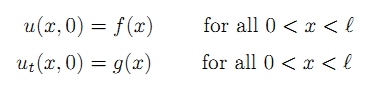
(2)边界条件:
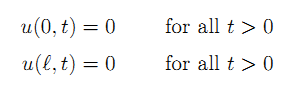
二,分步骤解答
第一步:方程的求解
(1)分离变量,并解出常系数普通偏微分方程的解:
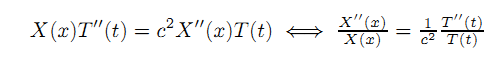
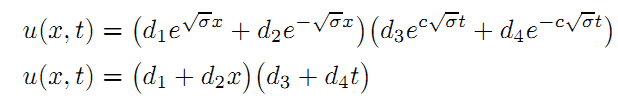
第二步:应用边界条件,缩小解的范围
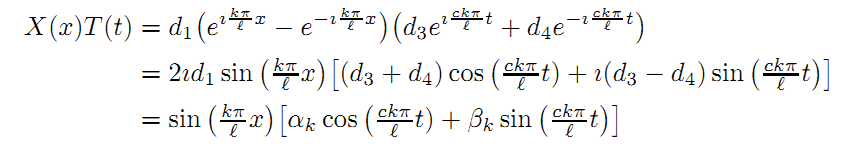
其中大括号内的两个常系数可以是任意数(包括复数)
第三步:应用初始条件,进一步缩小解的范围
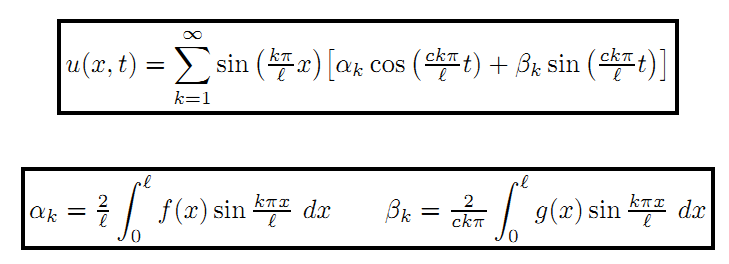
(1)固定时间t,当取不同的k值时,弦l会被划分成多个半周期,如下图,k分别取值1,2,3:

(2)固定位置x,略
三,小结
(1)不同的Mode,代表不同的k值,也即具有不同周期和频率的波;
(2)波动方程的解,可以看成是一系列三角函数的叠加;
四,参考资料
Joel Feldman, 2007. Solution of the Wave Equation by Separation of Variables.
Author: Crowboydoudou
Link: https://crowboydoudou.github.io/2018/12/04/分离变量法求解波动方程/
License: 知识共享署名-非商业性使用 4.0 国际许可协议