前言：

Representation theorem，表示定理，第一眼我看成了重构理论。正如《定量地震学》中所述，表示定理的是按照自己的意愿来处理地震学问题，将抽象问题转化为数学问题。具体的说，就是把震源的物理描述，及其在近处或远处的观测点产生运动的一般性问题，在数学的框架中描述出来。

问题：

（1）什么是表示定理？表示定理能做什么？

（2）在描述震源的过程表述定理干了什么事？

步骤：

一，最简单的表示定理

弹性动力学的表示定理包含以下两种类型（都存在对时间的依赖性）：（1）二维复平面中的表示定理；（2）三维空间中的表示定理

（1）二维复平面

若f(z)是复变量z的解析函数（analytical function），即满足下式：

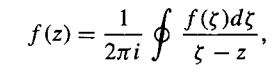
其中，积分回路可以是任意包含复变量z的路径，但是不能包含f的奇点。上式即是f(z)的一个表示，在确定f在C上的值后，却可以确定C内任意处的值。

（2）三维空间

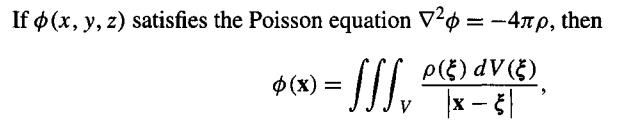
二，实际应用中的表示定理

首先，关注一个重要公式：互易定理。互易定理阐释了在任意弹性体V内一对解之间存在的一般关系。

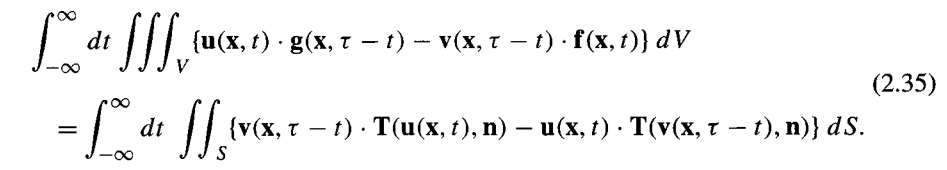
关于各参数的说明：

（1）u(x,t)，位移场中的一个，由体力f在考虑边界S上的及初始条件产生。T(u,n)由u产生的牵引力。

（3）v(x,t)，位移场中的一个，由体力g在于u不同的边界条件及初始条件下产生。T(v,n)由v产生的牵引力。

实际发现，以上表述方法非常难以理解。因此，这里寻求一种更加简洁易懂的方法，参考自《Seismic wave and sources》

1.明确问题

首先，我们需要知道表示定理的物理背景是什么？为什么需要表示定理。

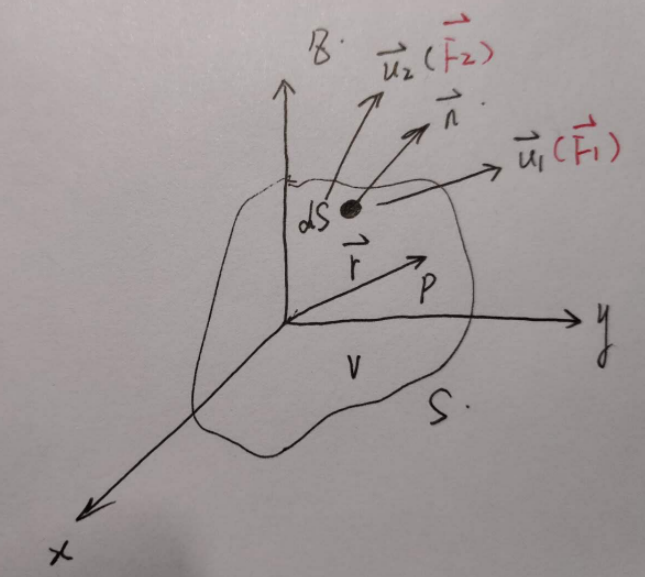
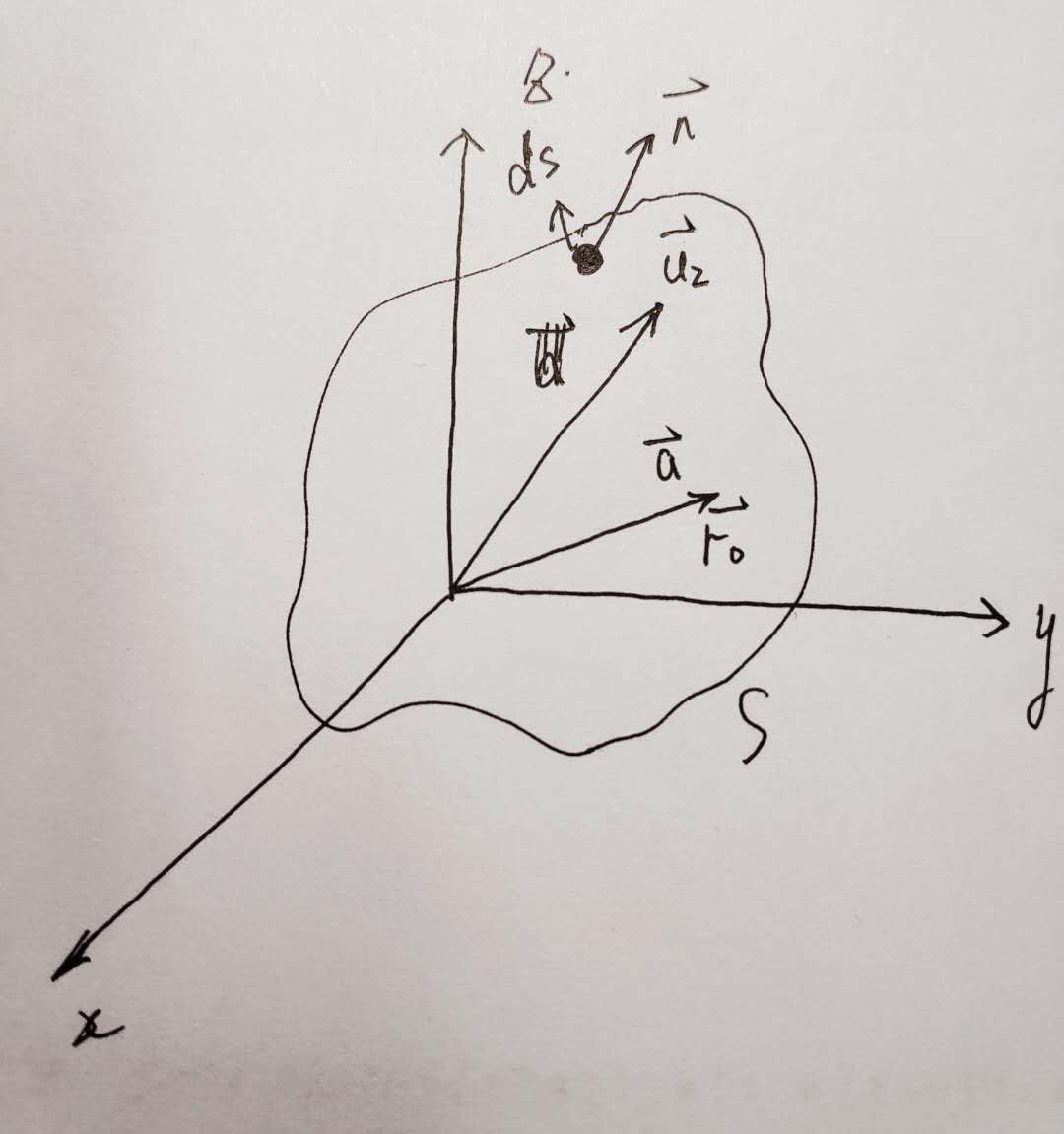
如图，假如源在原点处，那么，如何表示源在任意观测点（如r）处产生的位移u(x,t)。u1,u2表示体元V（包含面积S）上的任意两个矢量场（括号中为产生此应力场的单位体应力），n表示朝外的单位法向量。

正如这部分开头处提到的，u1,u2存在相应的数量关系，即Betti互异性定理：

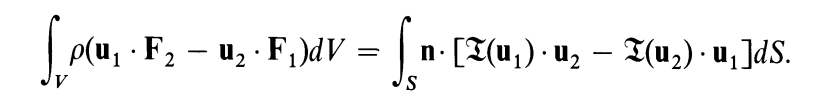
工字行符号表示应力，联系《定量地震学》中所述，应表示由位移产生的牵引力。可以看到，互异性定理描述了两组位移场间存在的力与位移之间的关系。左边是体积分，描述了两组体力与位移交叉相乘后再整个体积元内的影响；右面是面积分，描述了两组牵引力（实则是一个应力场在受体力而产生后由于牛顿第三定理而存在的反向作用力，这个作用力也会对其他位置产生影响）与位移之间的交叉相乘后在整个表面S上的影响（注意乘了一个法向矢量）。左边等于右边，可以说明三点：

（1）作用力与反作用之间的等效性；

（2）边界S上的连续性；

（3）能量的连续性，力*位移=动量

2.从已知位移场到任意位移场

假设在沿着r=a的r=r0处的单位体力（delta函数）在无限介质中产生了的位移场u2。同时假设无限介质的属性同互易定理下的模型中的有限介质V内的属性相同。首先，以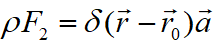替换上述互易定理，得到：

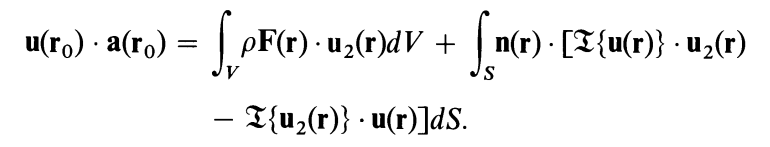
这称为索米亚那关系（Somigliana’s relation）

最后得到弹性动力学表示定理：

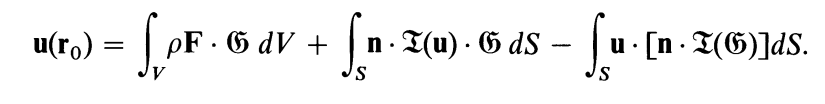
包含三部分：

第一项：体力分布在以格林函数的二阶导数作为权重时的体积分；即体力在位移场中的贡献值。

第二项：表面应力分布在以格林函数的二阶导数作为权重时的面积分；即表面应力在位移场中的贡献值。

第三项：表面位移场分布在以格林函数对应的牵引力与法向量的乘积作为权重时的面积分；即牵引力在位移场中的贡献值。

可以看到，格林函数更多的是充当了一个权重因子，均匀了体力、面力、牵引力的贡献。

最后，以森舍对表示定理的两条总结作结：

（1）表示定理的核心只有一个：牛顿第二定理

（2）表示定理共包含两个要素：一是震源，一是传播路径；综合考虑震源与传播路径，即是任意一点的位移

参考：

1. Ben-Menahem and Sarva Jit Singh. Seismic Waves and Sources.
2. Keiiti Aki, Paul G. Richards. Quantitative Seismology.
3. 陈运泰，顾浩鼎，震源理论基础（上册）.